
 |
Binääriluvut |
Binäärilukuja eli kaksijärjestelmää käytetään muun muassa tietokoneissa. Myös tavallinen valokytkin toimii binäärisenä kytkimenä, sillä siinä on kaksi asentoa.
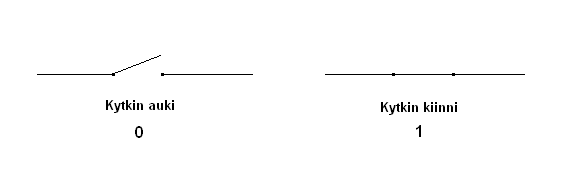
Kuvio 1: Yksinkertainen kytkin
Kun kytkin on auki eli asennossa 0, virta ei kulje lamppuun ja valo ei pala. Käännettäessä kytkin kiinni eli asentoon 1, virta pääsee kulkemaan ja valo lampussa palaa. Kaksijärjestelmän luvut voidaan esittää kuten kymmenjärjestelmän luvut kakkosen potenssin avulla. Esimerkiksi: 11002=1*23+1*22+0*21+0*20=1210. Kaksijärjestelmässä eli binäärijärjestelmässä on
Kymmenjärjestelmän lukuja voidaan muuttaa binääriluvuiksi jakojäännöksen avulla seuraavasti. Esimerkki: muutetaan luku 1210 binääriluvuksi. Jaetaan ensin kymmenjärjestelmän luku kantaluvulla 2 ja kirjataan ylös myös jakojäännös. Tämän jälkeen jaetaan jälleen edellisen jaon kokonaisosa kantaluvulla 2 ja samoin kuin edellä kirjataan myös jakojäännös muistiin. Näin jatketaan kunnes kokonaisosaksi jää luku 0.
12:2=6+0 -> kokonaisosa: 6, jakojäännös: 0
6:2=3+0 -> kokonaisosa: 3, jakojäännös: 0
3:2=1+1 -> kokonaisosa: 1, jakojäännös: 1
1:2=0+1 -> kokonaisosa: 0, jakojäännös: 1
Binääriesitys saadaan jakojäännöksistä kirjoittamalla jakojäännökset "alhaalta ylös" eli 1210=11002.
Binääriluvut puolestaan muutetaan kymmenjärjestelmän luvuiksi kakkosen potenssien avulla kuten edellä on esitetty. Esimerkiksi: 10101102=1*26+0*25+1*24+0*23+1*22+1*21+0*20=8610.
Ensimmäiset kahdeksan lukua voidaan esittää binäärilukuina seuraavasti:
| 010=0002 | 410=1002 |
| 110=0012 | 510=1012 |
| 210=0102 | 610=1102 |
| 310=0112 | 710=1112 |
| 1. 2110= | 6. 10010= |
| 2. 3310= | 7. 10110= |
| 3. 5610= | 8. 36510= |
| 4. 6910= | 9. 50510= |
| 5. 8610= | 10. 51110= |
| 1. 10112= | 6. 10111002= |
| 2. 100112= | 7. 11000002= |
| 3. 1001012= | 8. 1111000012= |
| 4. 1010012= | 9. 1110001112= |
| 5. 1010102= | 10. 111000102= |